有限域 Fp

• 當模數 p 是質數時，會創造出有限域 Fp。

• 包含 p 個元素：0, 1, 2, ..., p-1。

• 在這個域中的運算結果（加法、減法、乘法、除法）是封閉的，即結果仍然在這個集合中。

• 反元素:

  • 加法的時候逆元單位為0， 乘法的時候逆元單位為1
  • 加法反元素: 每個元素 a 都有一個加法反元素 b，使得 a + b = 0（mod p）。
  • 乘法反元素: 每個非零元素 a 都有一個乘法反元素 c，使得 a * c = 1(mod p）。

• 零因子: 在域中不存在零因子。

以下舉一個簡單例子方便理解有限域的概念:

F5（p = 5）

在 F5 中，元素是 0, 1, 2, 3, 4。

• 加法: 3 + 4 = 7，由於 7 超過了 4，所以我們將 7 mod 5，得到 2。因此，3 + 4 ≡ 2（mod 5）。
• 乘法: 2 * 3 = 6，同樣，6 超過了 4，所以我們將 6 mod 5，得到 1。因此，2 * 3 ≡ 1（mod 5）。這說明 2 的乘法逆元是 3。

環

• 當模數 n 不是質數時，模數 n 形成的結構是一個環。
• 反元素: 並非所有非零元素都有乘法逆元，即並非每個非零元素都存在 c 使得 a * c = 1（模 n）。
• 零因子: 環中可能包含零因子，這意味著存在兩個非零元素 a 和 b，使得 a * b = 0（模 n）。
  • eg: 在模 6 的環中，2 和 3 是零因子，因為 2 * 3 ≡ 0（模 6）。

以下舉一個簡單例子方便理解環的概念:

mod 6 的環

在 mod 6 的環中，元素是 0, 1, 2, 3, 4, 5。

• 加法: 2 + 4 = 6，6 mod 6 等於 0。因此，2 + 4 ≡ 0（mod 6）。
• 乘法: 2 * 3 = 6，6 mod 6 等於 0。因此，2 * 3 ≡ 0（mod 6）。這說明 2 和 3 是零因子。

而為什麼模數 n 是否為質數會影響結構？

這主要與質數唯一分解定理和乘法逆元有關。

質數模下的乘法逆元：

• 考慮一個質數 p，在模 p 的運算下，任意兩個不為 0 的元素 a 和 b，它們的乘積 a * b (mod p )必然不為 0（因為 p 是質數）。
• 由於 p 是質數，根據歐幾里得算法，一定存在整數 x 和 y，使得 ax + py = 1。
• 將上式取模 p，得到 ax ≡ 1 (mod p)。
• 這就說明，在模 p 的運算下，a 的乘法逆元是 x。
• 因此，在質數模下，每個非零元素都存在乘法逆元。

合數模下的乘法逆元：

• 考慮一個合數 n，它可以分解為若干個質數的乘積。
• 如果存在一個元素 a，使得 a 與 n 存在公因數 d > 1，那麼對於任意
  整數 x，ax ≡ 0 (mod d)，也就意味著 ax ≡ 0 (mod n)。
• 這表明，a 在模 n 的運算下沒有乘法逆元。
• 因此，在合數模下，不一定每個非零元素都存在乘法逆元。

費馬小定理

• 費馬小定理對於質數的判定非常有用，特別是要處理大數時。

• 條件: 如果 (a) 和 (p) 互質（即 gcd(a, p) = 1），且 (p) 是質數，則
  a^(p-1) ≡ 1 (mod p)

這表示當 (a) 和 (p) 互質時，將 (a) 的 (p-1) 次方取模 (p) 的結果總是 1。

不能逆推的說明

即使某個數 (a) 滿足 a^(p-1) ≡ 1 (mod p)，也不能保證 (p) 一定是質數。這是因為有些合數（例如 561）也會滿足這個條件。這些合數被稱為 卡邁克爾數，它們是費馬小定理的例外情況。

Modular Arithmetic 2

https://cryptohack.org/courses/modular/ma1/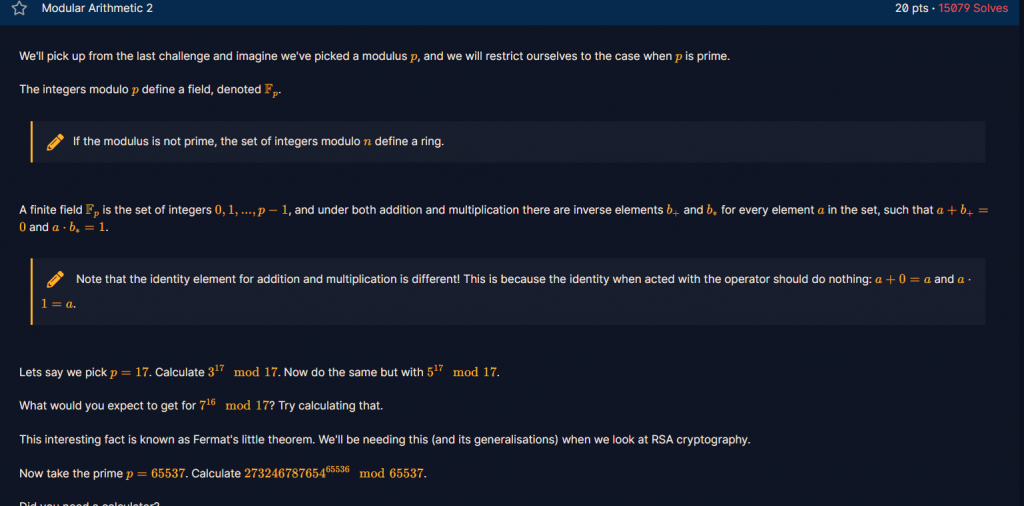

題意:

介紹了有限域和費馬小定理。
題目要我們計算273246787654^65536 mod 65537 。

解題過程:

套用費馬小定理，此時 a=273246787654, p=65537，所求= 1 mod p = 1

參考資料:

有限域:

• wiki: https://zh.wikipedia.org/zh-tw/%E6%9C%89%E9%99%90%E5%9F%9F
  逆元:
• https://zh.wikipedia.org/zh-tw/%E9%80%86%E5%85%83%E7%B4%A0 https://grorge.medium.com/%E8%A8%88%E7%AE%97%E6%A8%A1%E9%80%86%E5%85%83%E8%88%87%E4%B8%80%E4%BA%9B%E5%B8%B8%E7%94%A8%E7%9A%84%E7%AB%B6%E8%B3%BD%E6%95%B8%E5%AD%B8-ca0a1c001418
• https://oi-wiki.org/math/number-theory/inverse/
  費馬小定理:
• wiki: https://zh.wikipedia.org/zh-tw/%E8%B4%B9%E9%A9%AC%E5%B0%8F%E5%AE%9A%E7%90%86
• 詳細的內容: https://ithelp.ithome.com.tw/articles/10205906

後話:

今天寫了Modular-2，也順帶了解了費馬小定理、環與域以及逆元的概念。